Getrennte elektrische Ladungen bewirken das elektrische Feld. Die Intensität des Felds hängt davon ab, wie viel Ladung Q getrennt ist und wie weit die Ladungen voneinander entfernt sind. Es gilt die allgemeine Formel für die elektrische Feldstärke E:
Allgemeine elektrische Feldstärke
Die Feldstärke ist ein Vektor. Ihr Betrag gibt die Intensität des Felds an. Ihre Richtung gibt per Konvention die Richtung der Kraft an, die auf eine positive Ladung wirkt. Auf eine negative Ladung wirkt die Kraft des Felds in die entgegengesetzte Richtung. Die Wirkungsrichtung sollten Sie grundsätzlich mit Nachdenken ermitteln und nicht versuchen, sie aus dieser Formel zu gewinnen.
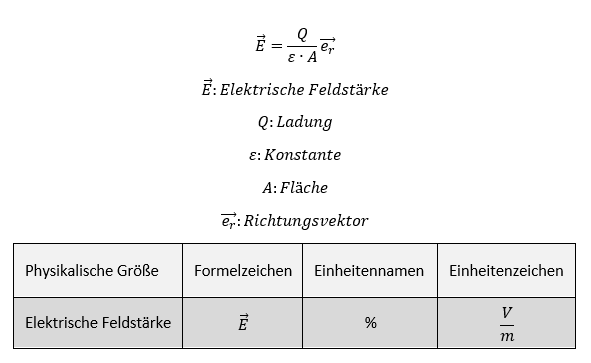
Betrachten wir zunächst das Feld einer Ladung Q1 im Raum. Wir bezeichnen eine Ladung als Punktladung, wenn die gesamte Ladungsmenge auf so wenig Fläche versammelt ist, dass die Geometrie als winziger Punkt betrachtet werden kann. Das ist die Quelle des elektrischen Felds. Das Feld wirkt im Raum. Je weiter wir uns von der Quelle entfernen, desto kleiner ist die Intensität des Felds. Das wird mathematisch dadurch ausgedrückt, dass die Fläche A, auf der das Feld wirkt, größer wird. Legen wir in Gedanken eine hohle Kugel um die Punktladung herum. Die Ladung bildet das Zentrum der Kugel. Dann sind alle Punkte der Kugeloberfläche gleich weit von der Ladung entfernt. Das Feld wirkt auf alle Punkte der Kugel gleich intensiv. Daraus leiten wir ab, wir die Intensität der Punktladung sich im Raum mit dem Abstand zur Ladung verändert: Wir setzen die Formel der Kugeloberfläche für A ein. Es gilt für das Feld der Punktladung Q1 die spezielle Formel:
Elektrische Feldstärke einer Punktladung
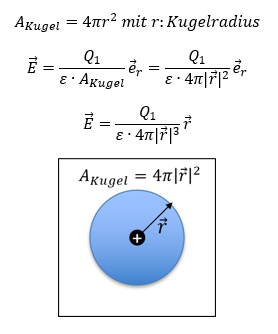
Wir führen jetzt eine Testladung Q2 ein. Die (angenommen) positive Punktladung Q1 stößt die positive Testladung Q2 ab. Die Richtung der Kraft auf Q2 weist dann in allen Richtungen radial von der Punktladung weg. Die Richtung der Kraft auf eine positive Testladung entspricht der Richtung des Felds. Deshalb ist der Richtungsvektor des Felds in der Formel gleich der Richtung des Radius r der Kugel. Wichtig: Das gilt nur bei Punktladungen. Die Formel für das Feld der Punktladung gibt die Intensität der Feldstärke für alle Punkte auf der Oberfläche einer Kugel mit Radius r an, deren Zentrum die Ladung Q1 ein ist.
Wäre die Punktladung Q1 negativ, würde die Kraft in allen Richtungen auf die Punktladung zuweisen. Die Richtung des Felds wird mit Feldlinien visualisiert. Feldlinien sind Pfeile im Raum, die die Richtung des Felds über die Pfeilrichtung angeben. In der unteren Abbildung sehen Sie die Felder einer positiven und einer negativen Punktladung im Raum.
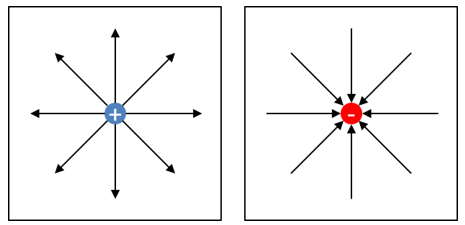
Die Intensität des Felds wird über die Dichte der Feldlinien dargestellt. Direkt an den Punktladungen sind viele Pfeile pro Fläche gezeichnet. Weiter weg nimmt die Dichte der Pfeile ab.
Das elektrische Feld ist abhängig vom Material zwischen den Ladungen. Es gibt Material, welches das Feld unverändert passieren lässt und anderes Material, welches es dämpft. Dies wird durch die Naturkonstante ε0 und den Materialparameter εr ausgedrückt. Für Vakuum (und näherungsweise auch für Luft) gilt εr = 1. Je mehr ein Material das Feld dämpft, desto größer wird εr. Es gilt also:
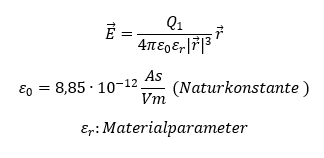
Die Materialeigenschaft der Feldstärke gilt allgemein und unabhängig von der Geometrie. Wir gehen dabei davon aus, dass stets der gesamte Bereich zwischen den Ladungen mit einem Material mit einem Wert von εr gefüllt ist. Sonst wird es etwas komplizierter.
Hinweis zu Formeln bei Feldern
Wie sie bereits in der Elektrostatik sehen gilt: Es gibt wenige allgemeine Formeln und viele Anwendungen auf spezielle Geometrien. Achten Sie darauf, welche Formeln allgemein sind und welche nur in bestimmten Kontexten gültig sind. Bei Feldern ist in nahezu allen Formeln mindestens ein Geometrie-Parameter enthalten, der – je nach Kontext – zu einer anderen Formel führt.
Weiter